Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 백준13417
- 백준3078
- ChatOpenAI
- 백준1720
- 백준3078 풀이
- 백준20126
- Frog River One
- LangChain
- 백준
- 두 개의 배열
- streamlit
- liquibse
- 백준17124
- 백준 타일코드
- BaseCallbackHandler
- 백준 도서관
- 백준16937
- 백준1461
- 백준1802
- 두 스티커
- 백준 시간초과
- java
- 외판원순회
- 교수님의 기말고사풀이
- generateChangeLog
- 백준2098
- 백준11332
- export changeLog
- streaming chat
- Codility
Archives
- Today
- Total
tempcru 삽질기록
[백준1720] 타일코드 문제 풀이 - JAVA 본문
[백준1720] 타일코드 문제 풀이 - JAVA
https://www.acmicpc.net/problem/1720
1720번: 타일 코드
2×N 크기의 넓은 판을 1×2 (또는 2×1) 크기와 2×2 크기의 타일로 채우려고 한다. 여러 가지 경우가 있을 수 있으므로, 각각을 하나의 코드로 대응시켜서 암호화에 이용하려고 한다. 그런데 문제가
www.acmicpc.net
타일 코드
시간 제한메모리 제한제출정답맞힌 사람정답 비율
| 2 초 | 128 MB | 3367 | 1401 | 1118 | 42.574% |
문제
2×N 크기의 넓은 판을 1×2 (또는 2×1) 크기와 2×2 크기의 타일로 채우려고 한다. 여러 가지 경우가 있을 수 있으므로, 각각을 하나의 코드로 대응시켜서 암호화에 이용하려고 한다.
그런데 문제가 생겼다. 넓은 판을 교환하다 보니 좌우 대칭인 경우가 있어, 뒤집히는 경우 코드가 헷갈리게 되는 경우가 발생한 것이다. 예를 들어 아래의 두 경우는 달라 보이지만 좌우 대칭을 이루고 있다.
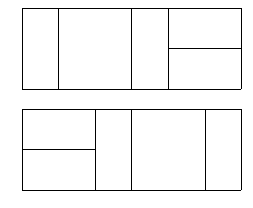
N이 주어지면, 전체 타일 코드의 개수를 구하는 프로그램을 작성하시오. (단, 서로 좌우 대칭을 이루는 중복된 표현은 한 가지 경우로만 처리한다.)
풀이
- 백준1793번 타일링 문제 업그레이드 버전이다
- 전형적인 DP 문제 = "이전에 계산한 답을 재활용할 수 있다"
- DP는 다이나믹 프로그래밍
- 다이나믹하다 = 가변적이다, 틀에박혀있지 않다
- 점화식 = 기존 답들을 활용해서 새로운 정답을 도출하기 위한 식
- 기존답을 활용하다보니 점화식은 f(x) = f(x-1) + f(x-2) 와 같이 우변에 기존 정답을 입력하곤 한다
- 무튼 이 문제도 DP문제인데 그이유는...
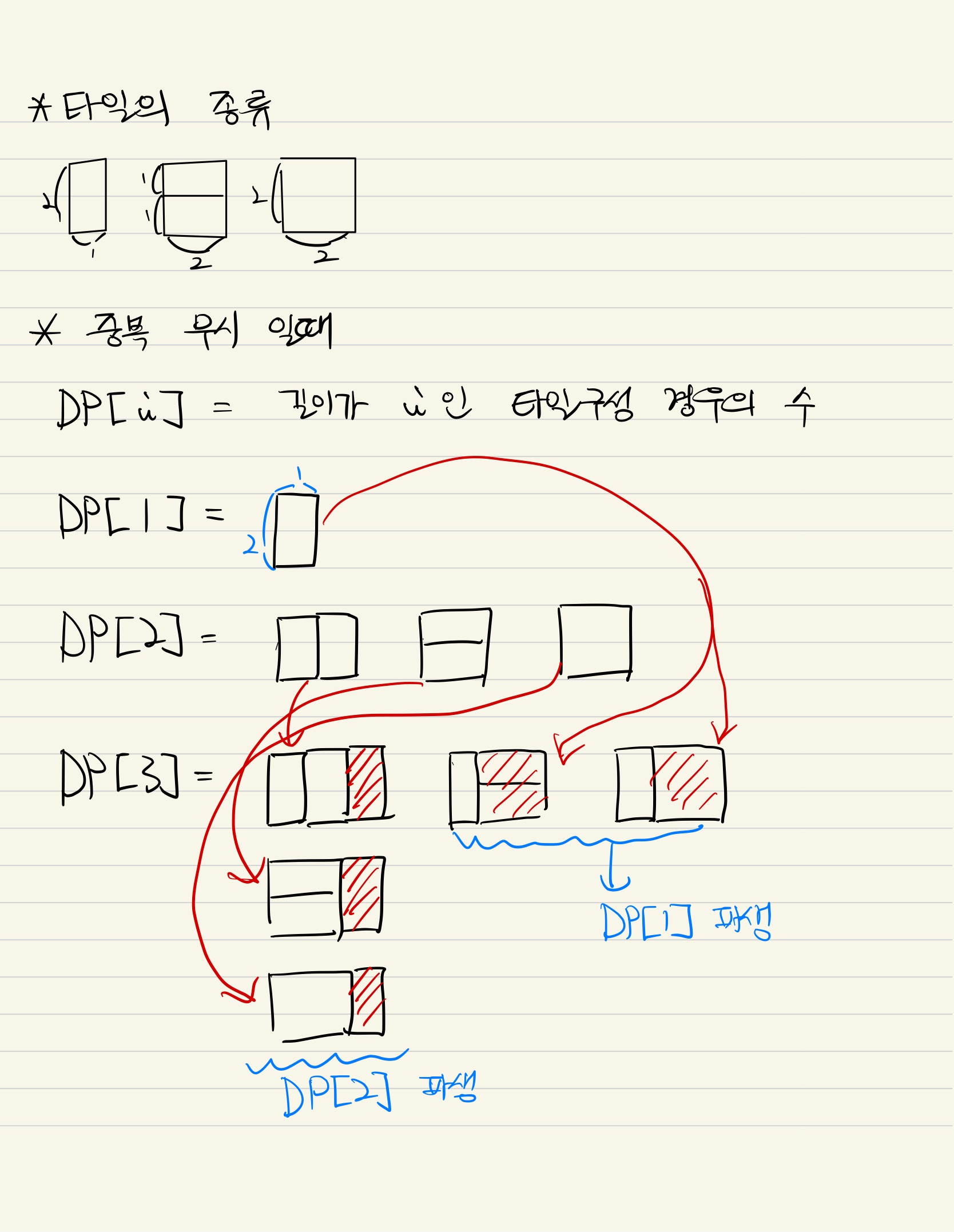
- DP[3]을 예로 들면 DP[3]은 DP[2] , DP[1] 에서 파생된 결과이다
- DP[2] 조합을 가지고 N = 3인 타일을 만들기 위해서는 2 x 1 타일 1개를 붙이면 된다
- DP[1] 조합을 가지고 N = 3인 타일을 만들기 위해서는 1 X 2 타일 과 2 X 2 등 2종류 타일을 붙이면된다
- 이것을 점화식으로 쓰면 DP[i] = DP[i-2] * 2 + DP[i-1] 이된다 // 1793번 답
- 길이가 i 인 타일조합은 어쨋든 i - 2 와 i - 1을 참고하면 되는 것이다
- 만약 타일의 길이가 더 다양했다면 점화식이 복잡해질꺼다
- 설명이 길었는데 문제에서는 중복처리문제도 있다.
- 중복처리를 위해서는 완전 대칭인 조합의 수를 찾아야한다
- DP[i] = i 길이인 모든 타일 조합이므로
- DP2[i] = i 길이인 뒤집어도 대칭인 조합을 찾는다
- DP2를 구하는 이유는 DP[i] - DP2[i] = 중복처리해야한 좌우 대칭 조합수 이기 때문이다
- DP[i] = 뒤집어도 똑같은 조합 + "뒤집으면 다른 조합" 이기 때문인데
- "뒤집으면 다른 조합"은 필연적으로 쌍을 이루기 때문이다
- DP2[i]는 홀수인 경우와 짝수인 경우 따로 생각해서 계산한다
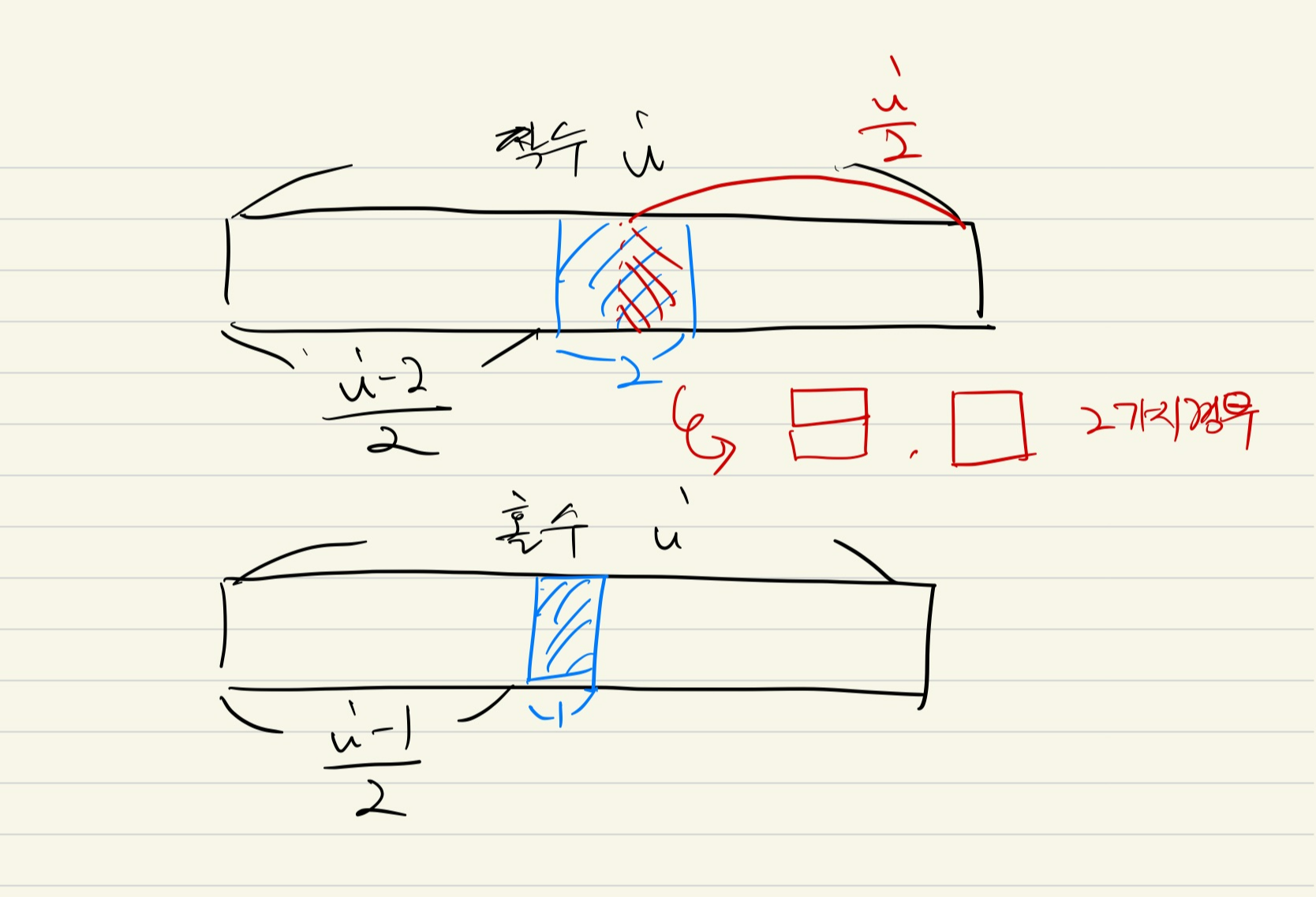
i == even 일때,
DP2[i] = DP[i/2] + DP[(i-2)/2] * 2 이다
DP[i/2]인 경우를 좌우대칭한 조합
DP[(i-2)/2] 좌우대칭에 1 X 2 사용조합
DP[(i-2)/2] 좌우대칭에 2 X 2 사용조합
i == odd 일때,
DP[(i-1)/2] 를 좌우대칭한 것과 같다
최종결과는 (DP[N] - DP2[N])/2 + DP2[N]; 하여 출력한다
package B1720;
import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
/**
* https://www.acmicpc.net/problem/1720
* title : 타일코드
* @author tempcru
*
* - 1793번 타일링 문제 업그레이드 버전 문제
* - 좌우 대칭인 경우, 중복을 제거하라는 문제
* - 좌우 대칭에 대한 처리를 홀수, 짝수로 나눠서 푼다
* - 완전대칭을 뒤집어도 같은 타일이라고 정의해본다
* - 정답 = (전체 타일 갯수 - 완전대칭)/2 + 완전대칭
* - 전체타일갯수에서 완전 대칭인 경우를 빼면 모두 일반적인 좌우대칭이므로 2로 나눠준다
*
*/
public class Main {
static int N;
static long result;
static long DP[];
static long DP2[];
public static void main(String[] args) throws Exception {
System.setIn(new FileInputStream("./src/B1720/sample_data"));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine().trim());
DP = new long[31];
DP2 = new long[31];
DP[0] = 1;
DP[1] = 1;
DP[2] = 3;
DP2[0] = 1;
DP2[1] = 1;
DP2[2] = 3;
for (int i = 3; i <= N; i++) {
DP[i] = DP[i-2]*2 + DP[i-1];
if(i%2 == 0) { // even
DP2[i] = DP[(i-2)/2]*2 + DP[i/2];
}else { // odd
DP2[i] = DP[(i-1)/2];
}
}
result = (DP[N] - DP2[N])/2 + DP2[N];
System.out.println(result);
}
}'Coding Test > 백준' 카테고리의 다른 글
| [백준16937] 두 스티커 문제풀이 - JAVA (0) | 2022.07.04 |
|---|---|
| [백준11332] 시간초과 문제 풀이 - JAVA (0) | 2022.07.01 |
| 백준3078 좋은 친구 문제 풀이 - JAVA (0) | 2022.06.09 |
| 백준13417 카드문자열 풀이 - java (0) | 2022.06.04 |
| 백준1461 도서관 문제 풀이 - java (0) | 2022.06.02 |

